СБОРНИК СТАТЕЙ
| Главная » Статьи » Всего статей |
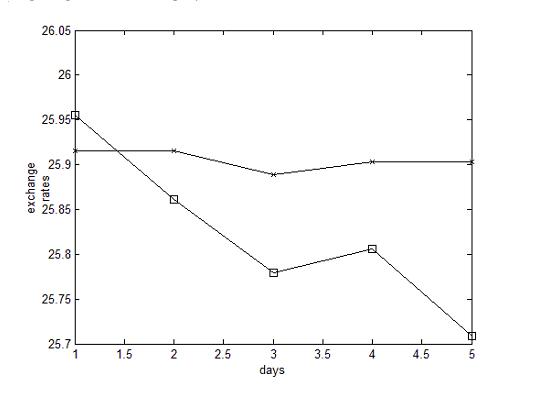
Проблема прогнозирования будущего является одной из важнейших проблем в различных областях человеческого знания. Если уравнения, описывающие процесс, не известны, то очень часто о процессе можно узнать по временным рядам одной или нескольких переменных, описывающих данный процесс. Характерной особенностью временных рядов в экономике является относительно небольшое число членов ряда (в отличие от рядов в физике). Данное обстоятельство ограничивает возможность выбора шага для прогноза по времени, а результаты анализа представляются менее надежными. Если во временных рядах экономических или иных численных данных велика составляющая чисто случайного, стохастического, процесса, то в таких случаях часто используют методы ARCH и GARCH. Если мы имеем дело с детерминированным процессом, то можно попытаться использовать метод ближайших соседей [1], [2]. Большой интерес представляет прогноз временных рядов обменных курсов валют. Российских исследователей особенно интересует обменные курсы доллара к рублю и евро к рублю. Для анализа таких экономических временных рядов в работе [3] использовались расчеты спектров мощностей, старших показателей Ляпунова и анализ главных компонент (SVD анализ). Проведенное исследование указало на наличие детерминированного хаоса в использованных временных рядах, что указало на возможность использования стандартного метода ближайших соседей [1]. В этом случае, согласно общепринятому подходу, временной ряд погружается в пространство размерности d, используя соседние члены данного ряда как компоненты d-мерного вектора. Далее рассматривается отображение последовательных d-мерных векторов друг на друга. Если величина d достаточно большая, то свойство такого дискретного отображения близко в топологическом смысле к свойствам неизвестной динамической системы с непрерывным временем, согласно теореме Такенса [4]. Далее у каждого d-мерного вектора находят число ближайших соседей (L), которые близки друг другу по норме, или же в других вариантах ближайшие соседи вычисляются по методу максимума коэффициентов корреляции. Одна часть ряда, таким образом, используется для нахождения размерности d, вторая часть ряда используется для нахождения коэффициентов линейного урав- нения регрессии, а третья часть временного ряда используется для составления прогноза. В данной работе предлагается определять размерность пространства погружения следуя [1], определяя ближайшее натуральное число к рассчитанной корреляционной размерности. Для анализа использовался временной ряд обменного курса доллара к рублю согласно Центробанку России с 1 января 2007 года до 26 мая 2007 года (итого 146 членов). Метод ближайших соседей был запрограммирован автором этого доклада в системе МАТЛАБ. Результаты прогноза на 5 дней вперед представлены на рисунке.
Обменный курс доллара к рублю: х - истинный, □ - предсказанный. Из рисунка видно, что некоторые детали поведения предсказываются методом ближайших соседей, использованным в данной работе автором. Можно высказать лишь предположения, что причины расхождения можно отнести как к недостаточно большому числу использованных членов ряда (146), так и к отсутствию динамики обменного курса в выходные дни. Литература 1. Farmer J.D., Sidorowich J.J. Predicting chaotic time series. //Physical Review letters, 1987. V. 59. N8. P.845-848. 4 2. Cao L., Soofi A.S. Nonlinear deterministic forecasting of daily dollar exchange rates. //International Journal of Forecasting, 1999. V. 18. P. 421-430. 3. Балонишников А.М., Балонишникова В.А. Моделирование динамики обменных курсов основных валют //Прикладная информатика, 2010. № 1. С. 15-20. 4. Takens F. Detecting strange attractors in turbulence. In : Rand D, Young L. (Eds.) Dynamical Systems in turbulence. Berlin: Springer-Verlag, 1981. Р. 336-381. | |
| Просмотров: 4693 | Комментарии: 2 | Теги: | Рейтинг: 4.0/1 |
| Всего комментариев: 2 | |
|
| |