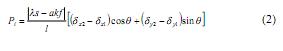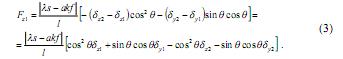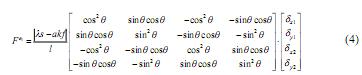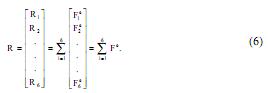СБОРНИК СТАТЕЙ
| Главная » Статьи » Всего статей |
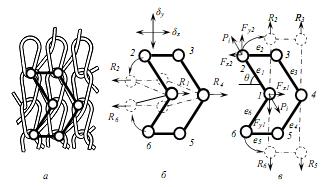
Текстильные конструкционные композиты представляют собой материалы на основе армирующих каркасов (волокнистого слоя, ткани, нетканого полотна, трикотажа) и матриц из связующего материала. Уникальное сочетание легкости, гибкости, высокой прочности и внутренней вязко- 84 сти, характерное для текстильных армирующих структур, определило преимущества применения композитов для широкого спектра изделий: в автомобиле- и судостроении, для изготовления судовых корпусов и ненесущих деталей авто; в строительстве, в том числе для армирования бетонных конструкций; а также в средствах индивидуальной защиты от механических и тепловых воздействий. Трикотажные структуры, позволяют реализовать значительно более широкий диапазон форм и свойств, чем тканые. К примеру, простые осно-вовязаные и уточно-вязанные (кулирные) структуры обеспечивают деформируемость полотна во всех направлениях и, следовательно, пригодны для изготовления композитных изделий глубоким формованием. Кулирному и основовязаному трикотажу можно придать определенную деформируемость в определенных направлениях, придать стабильность размеров в одном направлении и способность к формованию в других. При разрушении композиты не образуют осколков, что снижает опасность травматизма при различных авариях. В настоящее время текстильные конструкционные композиты представляют собой небольшую, но технически важную часть быстро развивающейся области текстильных композитов. 4 б в а Структура ячейки основовязаного трикотажа (трико) и ее шарнирно-стержневой эквивалент В данной работе предлагается методика матричного расчета механических свойств основовязаного трикотажа на основе метода конечных элементов. Основовязаные полотна имеют одинаковую растяжимость в обоих направлениях, поэтому они предпочтительны при формовании объемных композитных деталей. В качестве конечного элемента принята петля, как элементарная ячейка трикотажной структуры (рисунок). Также разработана динамическая имитационная модель поведения трикотажной структуры при воздействии нагрузок.
Структура ячейки основовязаного трикотажа (трико) и ее шарнирно-стержневой эквивалент При использовании трикотажных полотен в качестве текстильной основы для композитных материалов важно знать, как поведет себя полотно при объемном формовании композитного изделия, а также при дальнейшей эксплуатации под действием многоцикловых или разрушающих нагрузок. Для полного описания физико-механических свойств модели применим способ разбиения на элементарные шестизвенные элементы, состоящие из стержней (имитирующих нити) и шарниров (имитирующих место перегиба нити в петле), обладающих упруго-гибкими свойствами. Трикотажные полотна по сравнению с тканью имеют большую растяжимость, поскольку в трикотажной петле при общей деформации происходит не только растяжение нити, но и ее изгиб, с перемещением точек фиксации между нитями соседних петель и увеличением размеров самой петли. Поэтому перед рассмотрением деформации всего полотна необходимо проанализировать упругие свойства элементарной ячейки, которые не могут быть изотропными. Как и многие текстильные полотна, трикотаж можно представить в виде плоской сетки или в виде ячеистой структуры. Механические свойства ячейки основовязаной структуры в соответствии с методом конечных элементов были представлены в виде матрицы жесткости, при продольном и поперечном растяжении.
Продольная сила Р, приложенная к стержню, будет определяться выражением:
где s - площадь поперечного сечения стержня (нити), к - модуль упругости нити, k - коэффициент трения между нитями в узлах ячейки, f - площадь поверхности трения, a - коэффициент, учитывающий увеличение трения между нитями в узлах, по мере их натяжения при деформации ячейки, а = а (Sxt, Syi). В матричном виде выражение (2) запишется следующим образом:
или
Если матрица в выражении (4) симметрична, то можно записать матричное выражение для элемента е1
Результирующая система уравнений в матричном виде может быть записана следующим образом:
Матричные операции и наглядное представление данной модели как стержневой системы было реализовано в программной среде MatLab 6.5. (пакет Simulink 4.0) Конечно-элементное, моделирование текстильных структур - композитов, армированных текстильными материалами. В настоящее время это интенсивно развивающееся направление механики композитов и текстиля. С целью облегчения матричного расчета элементарной ячейки трикотажного полотна и подтверждения адекватности, разрабатываемых конечно-элементных моделей был создан программный продукт на основе языка программирования Visual Basic, позволяющий получить итоговые данные расчетов результирующих нагрузок и деформаций при растяжении трикотажного полотна. Для ускорения поиска и ввода в программу исходных данных была создана база данных. Данная база была сформирована на основе средства разработки Microsoft Access 2003 в виде авторского программного продукта, для дальнейшего использования в программной среде Visual Basic 6.0. База включает в себя такие исходные параметры текстильных материалов, как s - площадь поперечного сечения стержня (нити), к - модуль упругости нити, k - коэффициент трения между нитями в узлах ячейки, j - площадь поверхности трения, а - коэффициент, учитывающий увеличение трения между нитями в узлах в результате продольно-поперечных деформаций. База включает в себя итоговые данные расчетов результирующих нагрузок и деформаций при растяжении трикотажного полотна. Результаты моделирования на уровне ячейки периодической структуры трикотажного полотна и макрорасчеты упругих свойств трикотажа дают возможность проектирования армирующего волокнистого наполнителя композиционных материалов с прогнозированием его механических характеристик. | |
| Просмотров: 2271 | Комментарии: 1 | Теги: | Рейтинг: 0.0/0 |
| Всего комментариев: 0 | |